滤波器设计教程

作者： Moto Hira

本教程介绍如何创建基本的数字滤波器 （脉冲响应）及其属性。

我们根据 windowed-sinc 内核和频率采样方法。

警告

本教程需要原型 DSP 功能，这些功能是 在 nightly 版本中可用。

请参阅 https://pytorch.org/get-started/locally 有关安装 nightly 版本的说明。

import torch
import torchaudio

print(torch.__version__)
print(torchaudio.__version__)

import matplotlib.pyplot as plt

2.4.0
2.4.0

from torchaudio.prototype.functional import frequency_impulse_response, sinc_impulse_response

Windowed-Sinc 滤波器

Sinc 滤波器是一种 理想化滤波器，可去除截止频率以上的频率 频率，但不影响较低的频率。

Sinc 滤波器在解析解中具有无限的滤波器宽度。 在数值计算中，sinc 滤波器不能精确表示， 所以需要一个近似值。

窗 sinc 有限脉冲响应是 sinc 的近似值 滤波器。它是通过首先计算给定的 sinc 函数获得的 截止频率，然后截断滤波器裙边，以及 应用窗口（如 Hamming 窗口）来减少 从 Truncation 引入的工件。

为给定的截止生成 windowed-sinc 脉冲响应 频率。

低通滤波器

脉冲响应

创建 sinc IR 就像将截止频率值传递给 一样简单。

cutoff = torch.linspace(0.0, 1.0, 9)
irs = sinc_impulse_response(cutoff, window_size=513)

print("Cutoff shape:", cutoff.shape)
print("Impulse response shape:", irs.shape)

Cutoff shape: torch.Size([9])
Impulse response shape: torch.Size([9, 513])

让我们可视化生成的脉冲响应。

def plot_sinc_ir(irs, cutoff):
    num_filts, window_size = irs.shape
    half = window_size // 2

    fig, axes = plt.subplots(num_filts, 1, sharex=True, figsize=(9.6, 8))
    t = torch.linspace(-half, half - 1, window_size)
    for ax, ir, coff, color in zip(axes, irs, cutoff, plt.cm.tab10.colors):
        ax.plot(t, ir, linewidth=1.2, color=color, zorder=4, label=f"Cutoff: {coff}")
        ax.legend(loc=(1.05, 0.2), handletextpad=0, handlelength=0)
        ax.grid(True)
    fig.suptitle(
        "Impulse response of sinc low-pass filter for different cut-off frequencies\n"
        "(Frequencies are relative to Nyquist frequency)"
    )
    axes[-1].set_xticks([i * half // 4 for i in range(-4, 5)])
    fig.tight_layout()

plot_sinc_ir(irs, cutoff)

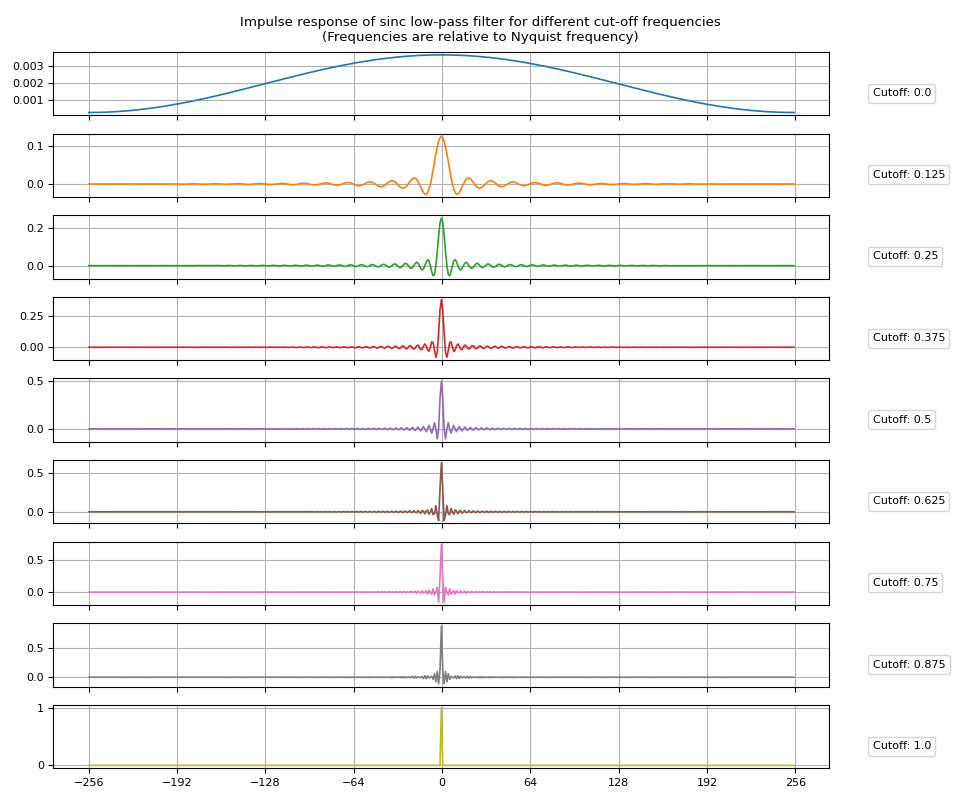
频率响应

接下来，我们来看一下频率响应。 Simpy 将傅里叶变换应用于脉冲响应将得到 频率响应。

frs = torch.fft.rfft(irs, n=2048, dim=1).abs()

让我们可视化生成的频率响应。

def plot_sinc_fr(frs, cutoff, band=False):
    num_filts, num_fft = frs.shape
    num_ticks = num_filts + 1 if band else num_filts

    fig, axes = plt.subplots(num_filts, 1, sharex=True, sharey=True, figsize=(9.6, 8))
    for ax, fr, coff, color in zip(axes, frs, cutoff, plt.cm.tab10.colors):
        ax.grid(True)
        ax.semilogy(fr, color=color, zorder=4, label=f"Cutoff: {coff}")
        ax.legend(loc=(1.05, 0.2), handletextpad=0, handlelength=0).set_zorder(3)
    axes[-1].set(
        ylim=[None, 100],
        yticks=[1e-9, 1e-6, 1e-3, 1],
        xticks=torch.linspace(0, num_fft, num_ticks),
        xticklabels=[f"{i/(num_ticks - 1)}" for i in range(num_ticks)],
        xlabel="Frequency",
    )
    fig.suptitle(
        "Frequency response of sinc low-pass filter for different cut-off frequencies\n"
        "(Frequencies are relative to Nyquist frequency)"
    )
    fig.tight_layout()

plot_sinc_fr(frs, cutoff)

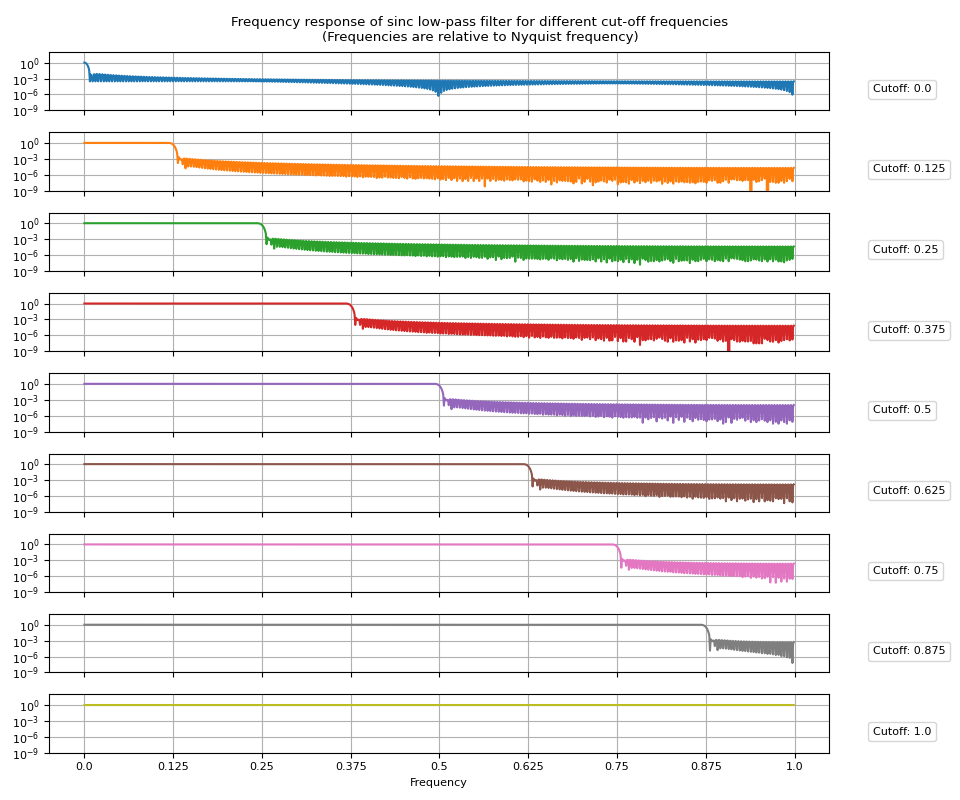
高通滤波器

高通滤波器可以通过减去低通来获得 来自 Dirac delta 函数的脉冲响应。

传递给 会将返回的 filter 内核更改为 high pass filter。high_pass=True

irs = sinc_impulse_response(cutoff, window_size=513, high_pass=True)
frs = torch.fft.rfft(irs, n=2048, dim=1).abs()

脉冲响应

plot_sinc_ir(irs, cutoff)

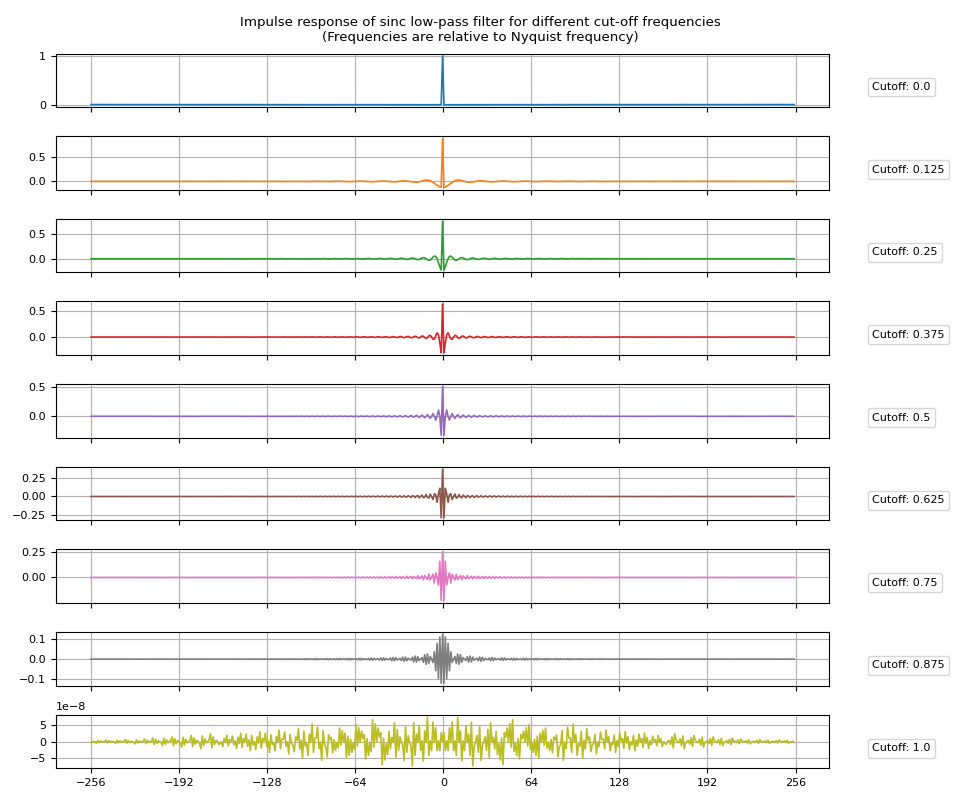
频率响应

plot_sinc_fr(frs, cutoff)

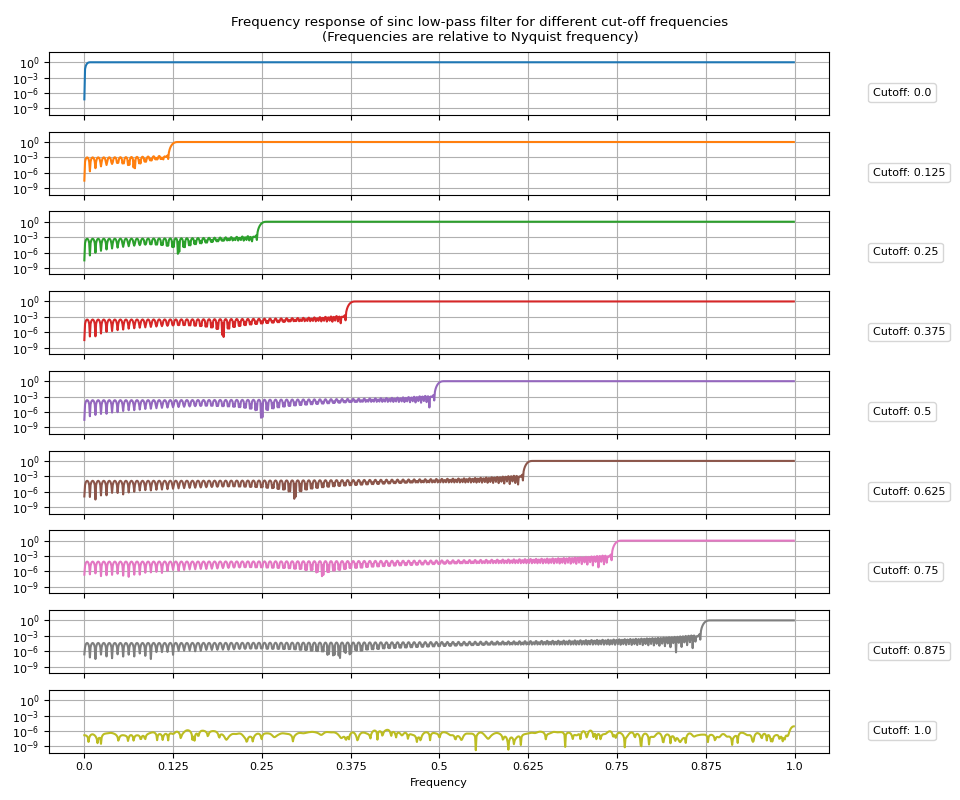
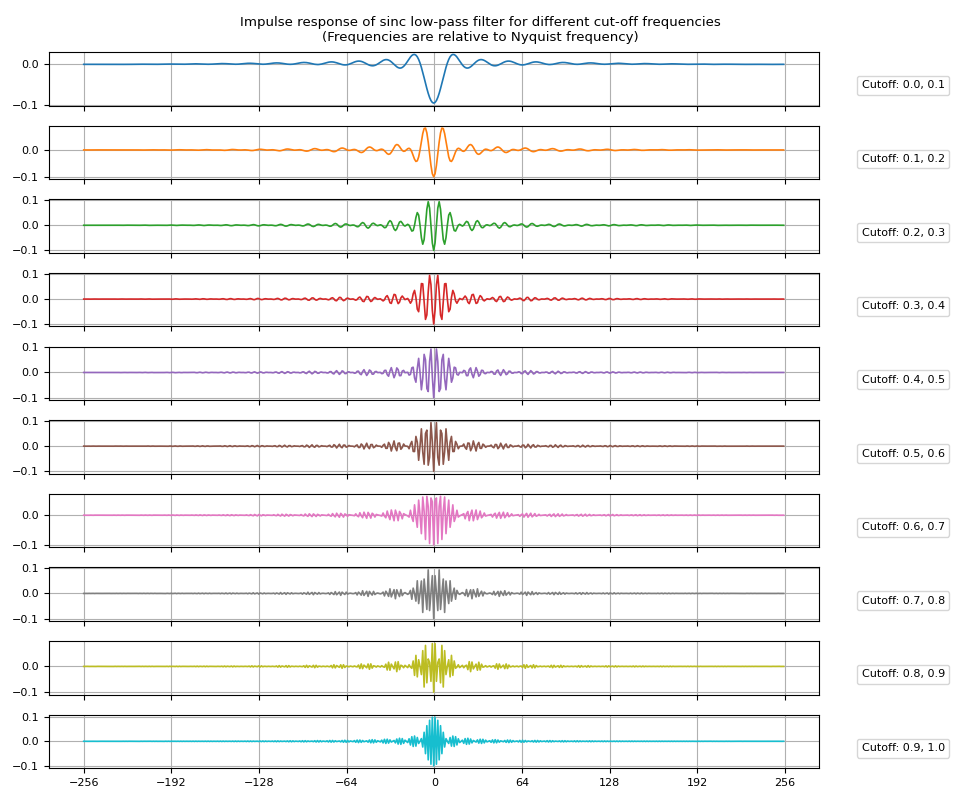
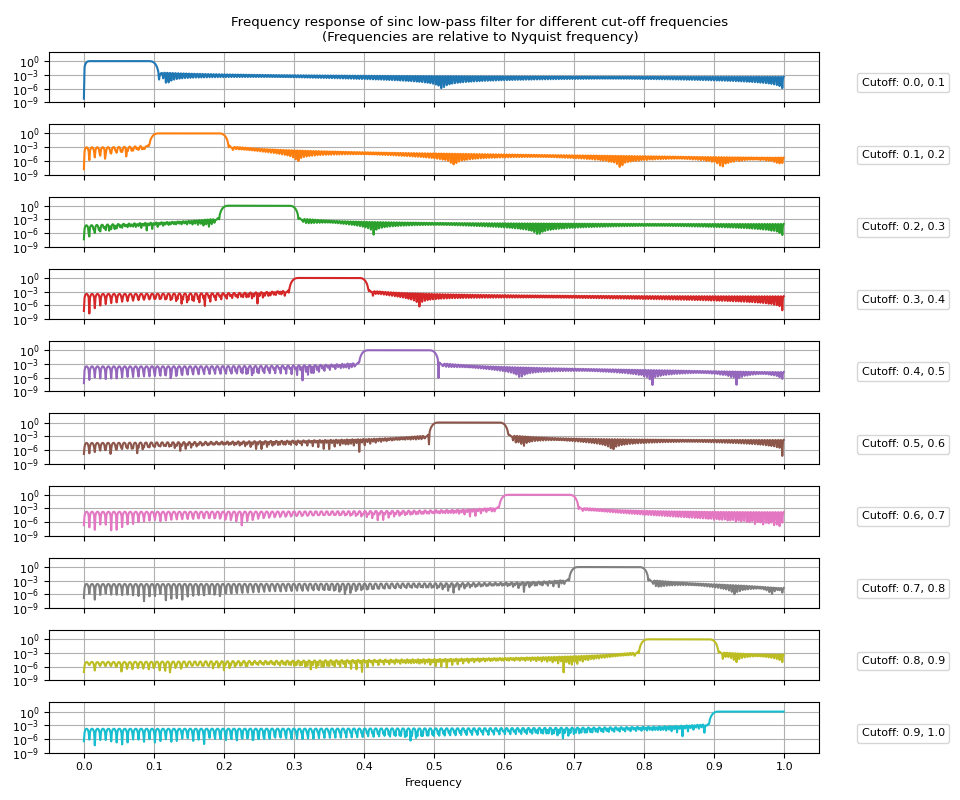
带通滤波器

带通滤波器可以通过减去 上带与下带的上带。

cutoff = torch.linspace(0.0, 1, 11)
c_low = cutoff[:-1]
c_high = cutoff[1:]

irs = sinc_impulse_response(c_low, window_size=513) - sinc_impulse_response(c_high, window_size=513)
frs = torch.fft.rfft(irs, n=2048, dim=1).abs()

脉冲响应

coff = [f"{l.item():.1f}, {h.item():.1f}" for l, h in zip(c_low, c_high)]
plot_sinc_ir(irs, coff)

频率响应

plot_sinc_fr(frs, coff, band=True)

频率采样

我们研究的下一个方法从所需的频率响应开始 并通过应用逆傅里叶变换来获得脉冲响应。

取频率的 （非规范化） 幅度分布，并且 从中构造脉冲响应。

但请注意，生成的脉冲响应不会产生 所需的频率响应。

在下文中，我们将创建多个过滤器并比较输入 频率响应和实际频率响应。

砖墙过滤器

让我们从砖墙过滤器开始

magnitudes = torch.concat([torch.ones((128,)), torch.zeros((128,))])
ir = frequency_impulse_response(magnitudes)

print("Magnitudes:", magnitudes.shape)
print("Impulse Response:", ir.shape)

Magnitudes: torch.Size([256])
Impulse Response: torch.Size([510])

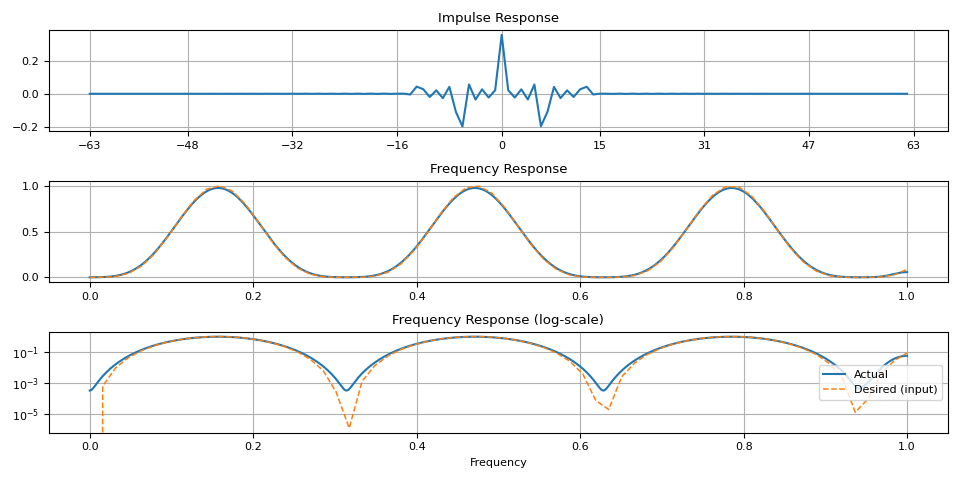
def plot_ir(magnitudes, ir, num_fft=2048):
    fr = torch.fft.rfft(ir, n=num_fft, dim=0).abs()
    ir_size = ir.size(-1)
    half = ir_size // 2

    fig, axes = plt.subplots(3, 1)
    t = torch.linspace(-half, half - 1, ir_size)
    axes[0].plot(t, ir)
    axes[0].grid(True)
    axes[0].set(title="Impulse Response")
    axes[0].set_xticks([i * half // 4 for i in range(-4, 5)])
    t = torch.linspace(0, 1, fr.numel())
    axes[1].plot(t, fr, label="Actual")
    axes[2].semilogy(t, fr, label="Actual")
    t = torch.linspace(0, 1, magnitudes.numel())
    for i in range(1, 3):
        axes[i].plot(t, magnitudes, label="Desired (input)", linewidth=1.1, linestyle="--")
        axes[i].grid(True)
    axes[1].set(title="Frequency Response")
    axes[2].set(title="Frequency Response (log-scale)", xlabel="Frequency")
    axes[2].legend(loc="center right")
    fig.tight_layout()

plot_ir(magnitudes, ir)

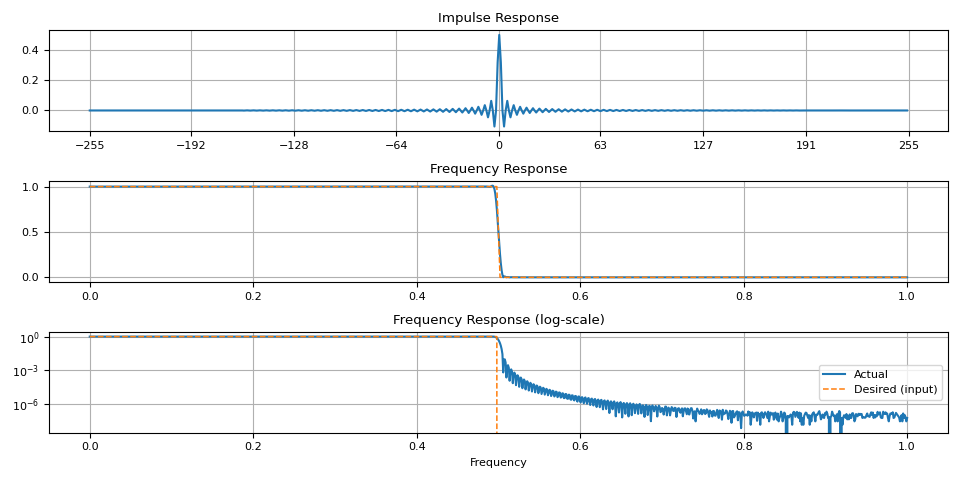
请注意，过渡带周围有伪影。这是 当窗口较小时更明显。

magnitudes = torch.concat([torch.ones((32,)), torch.zeros((32,))])
ir = frequency_impulse_response(magnitudes)

plot_ir(magnitudes, ir)

任意形状

magnitudes = torch.linspace(0, 1, 64) ** 4.0
ir = frequency_impulse_response(magnitudes)

plot_ir(magnitudes, ir)

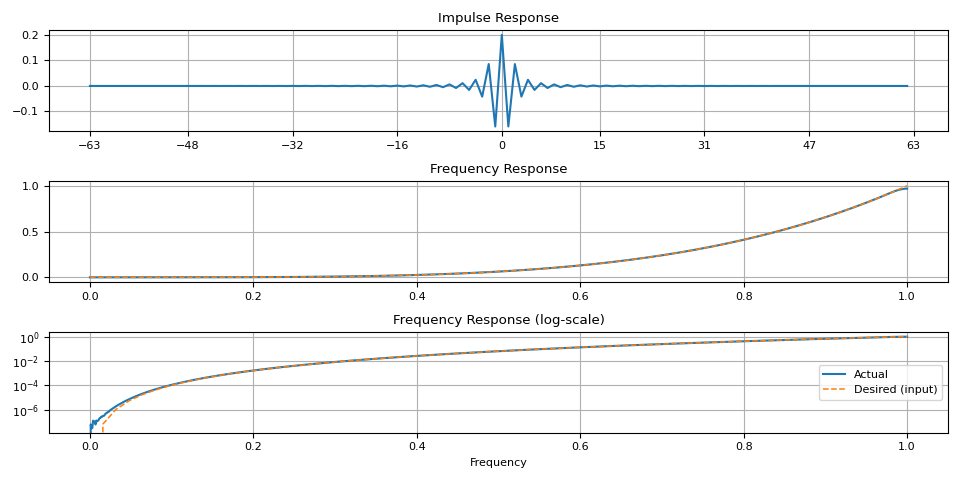
magnitudes = torch.sin(torch.linspace(0, 10, 64)) ** 4.0
ir = frequency_impulse_response(magnitudes)

plot_ir(magnitudes, ir)

引用

• https://en.wikipedia.org/wiki/Sinc_filter

• https://www.analog.com/media/en/technical-documentation/dsp-book/dsp_book_Ch16.pdf

• https://courses.engr.illinois.edu/ece401/fa2020/slides/lec10.pdf

• https://ccrma.stanford.edu/~jos/sasp/Windowing_Desired_Impulse_Response.html